Abrir ventana de notas Activar notas al lado Introducción

Métodos

Resultados

Aplicabilidad de la teoría de elasticidad no local en comportamiento mecánico de sólidos usando FEM

Arturo Rodriguez
da.rodriguezh@uniandes.edu.co

Fernando Ramirez
f.ramirez@uniandes.edu.co

Introducción

Métodos

Resultados

Introducción

Métodos

Resultados

Teoría no local

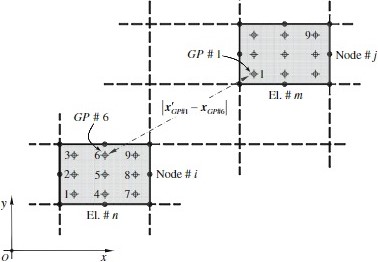
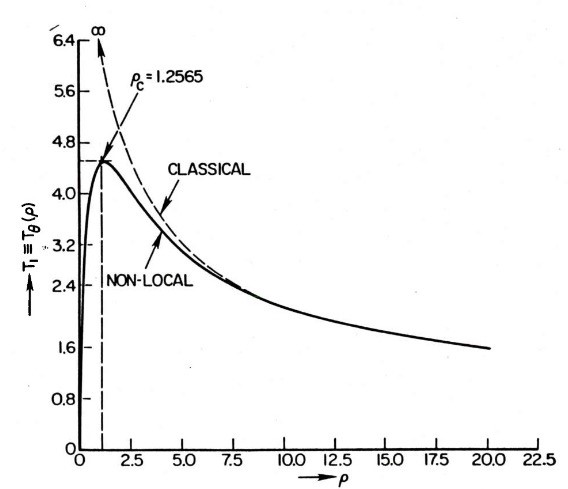
Interacción de largo alcance entre elementos. Tomado de Pisano et al. (2009)

Comparación entre esfuerzos cortantes producidos por una carga puntual. Tomado de Eringen (1987)

La teoría clásica no logra predecir el comportamiento a escala nano métrica (Fleck et al., 1994; Stölken & Evans ,1998; Ramirez, 2006) \[{\Large\sigma_{ij}=C_{ijkl}\varepsilon_{kl}}\]

Tener en cuenta las fuerzas de cohesión de largo alcance entre partículas (Eringen, 1983) \[{\Large\sigma_{ij}=\int_{\Omega}\alpha(\rho)C_{ijkl}\varepsilon'_{kl}dv'}\]

Notas presentación
- Local no predice comportamiento a nano escala
- Eringen 1987, interacciones de largo alcance
- Singularidades de esfuerzos
- Modificación a la ecuación constitutiva

Notas extendido
Que es la teoría no local

El comportamiento mecánico de materiales en dimensiones muy pequeñas es diferente de su comportamiento a macro escala. Por lo tanto, las teorías clásicas de elasticidad no pueden predecir el comportamiento de los materiales a escala nano métrica. En consecuencia, se han desarrollado varias teorías para predecir el comportamiento mecánico de materiales a nano escala.

Una de estas teorías es la teoría no local de elasticidad, desarrollada principalmente por Eringen en 1972. Esta teoría logra incluir los efectos de fuerzas cohesivas de largo alcance en la modelación del medio continuo.

Frase obligatoria

No local es modificación a ley constitutiva.

Introducción

Métodos

Resultados

Teoría no local

Pandeo de nanotubos. Tomado de Gormani et al. (2021)

Frecuencias de placa. Tomado de Shariati et al. (2021)

Soluciones para vigas. Tomado de Wang et al. (2016)

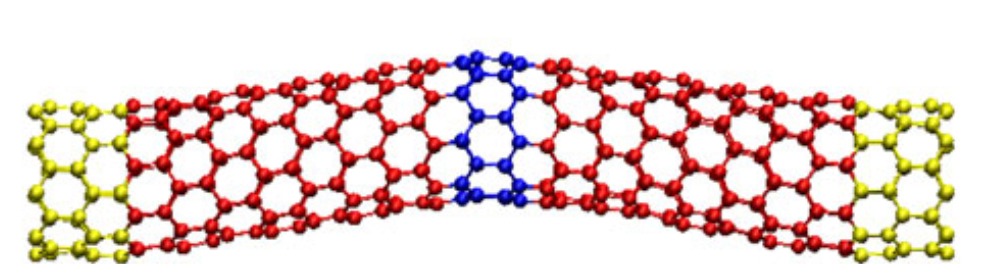
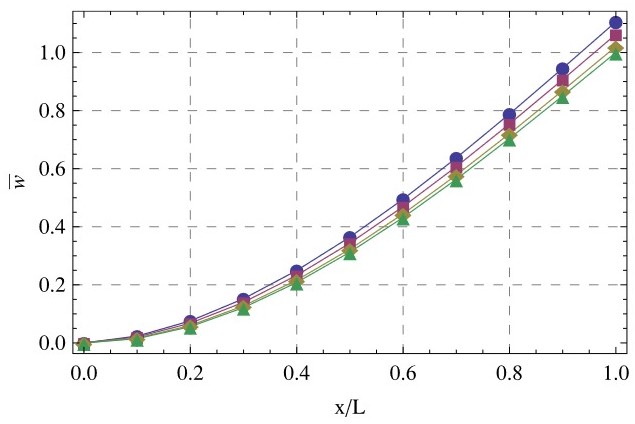
Se encontró que la carga crítica de pandeo disminuye cuando se tienen en cuenta los efectos no locales

Se compararon las frecuencias de vibración no locales con las encontradas usando dinámica molecular

Soluciones analíticas para vigas con distintas condiciones de apoyo. Los desplazamientos aumentan al tener en cuenta no local

Gran costo computacional!

Notas presentación
- Análisis 1D y 2D
- Disminución de rigidez
- Dinámica molecular
- Costo computacional menor al de DM pero mayor comparado con análisis normal
- Los efecto no locales disminuyen aumentando el tamaño del dominio

Notas extendido
Aplicaciones

La teoría no local de elasticidad ha sido usada en distintas aplicaciones de ingeniería como: En la figura 3 podemos apreciar un análisis de pandeo en nanotubos de carbono teniendo en cuenta no local, realizado por Gormani en 2021. Se encontró que teniendo en cuenta la no localidad disminuía la carga crítica de pandeo de los nanotubos.

Figura 4: Análisis de frecuencias en placa de grafeno redonda comparando los resultados con dinámica molecular.

Figura 5: Se han desarrollado varias soluciones analíticas para vigas, obteniendo deflexiones mayores bajo todas las condiciones de borde a excepción de una viga simplemente apoyada, donde se encontraron deflexiones menores.

Frases obligatorias
La no localidad DISMINUYE la rigidez.
Los estudios de frecuencias solo se han realizado en 2D y 3D.
La mayoría de estos estudios son analíticos.

Introducción

Métodos

Resultados

¿Qué tamaño es suficiente para no tener en cuenta los efectos no locales?

Introducción

Métodos

Resultados

Objetivo

Encontrar el tamaño para el cual no es relevante usar la teoría no local

¿Cómo?

Frecuencias para nanopartículas (cubos, esferas o tetraedros)
Frecuencias para placas
Frecuencias para vigas

Introducción

Métodos

Resultados

Metodología

Introducción

Métodos

Resultados

Teoría no local integral

Teoría integral (Eringen & Edelen, 1972)

\[\scriptsize{\sigma_{ij}=\int_{\Omega}\alpha(\rho)C_{ijkl}\varepsilon'_{kl}dv'}\]

Teoría diferencial (Eringen, 1983)

\[\scriptsize{(1-e_0a\nabla^2)\sigma_{ij}=C_{ijkl}\varepsilon_{kl}}\]

Modelo integral de dos fases (Polizzotto, 2001)

\[\scriptsize{\sigma_{ij}=\zeta_1 C_{ijkl}\varepsilon_{kl} + \zeta_2\int_{\Omega}A(\rho)C_{ijkl}\varepsilon'_{kl}dv'}\]

Notas presentación
- Modelo original (integral) 1972, Eringen
- Modelo diferencial 1983, Eringen. Facilitar manipulación algebraica
- Soluciones analíticas generalmente diferencial
- Modelo dos fases 2001, Polizzotto. Facilita la implementación numérica.
- Usar modelo dos fases

Notas extendido
Modelos constitutivos no locales

A lo largo de los años, la teoría no local de Eringen ha evolucionado, del modelo original de elasticidad no local se derivan el modelo integral (EQ 1) y la teoría diferencial (EQ 2).

La teoría integral es básicamente la teoría original sin aliteraciones, la teoría diferencial es un caso específico de la ecuación constitutiva original que permite una manipulación matemática mas sencilla.

Esto ha llevado a que la mayoría de los estudios y comprobaciones de esta teoría se realicen usando el modelo diferencial.

Recientemente, se propuso un modelo integral de dos fases, donde el material se modela como un material compuesto que tiene una parte local y una parte no local. Dicho modelo tiene ventajas en su implementación computacional

Frases obligatoria
Las 3 ecuaciones son modelos distintos que provienen de una teoría mas grande

Los modelos hijos de no local nunca dan lo mismo. Son teorías distintas

Introducción

Métodos

Resultados

Parámetros del modelo no local

\[\scriptsize{\sigma_{ij}=\zeta_1 C_{ijkl}\varepsilon_{kl} + \zeta_2\int_{\Omega}A(\rho)C_{ijkl}\varepsilon'_{kl}dv'}\]

Introducción

Métodos

Resultados

Parámetros del modelo no local

\[\scriptsize{\sigma_{ij}={\color{lightgray} \zeta_1} C_{ijkl}\varepsilon_{kl}+ {\color{lightgray} \zeta_2\int_{\Omega}A(\rho)C_{ijkl}\varepsilon'_{kl}dv'}}\]

Introducción

Métodos

Resultados

Parámetros del modelo no local

\[{\color{lightgray}\scriptsize{\sigma_{ij}= \zeta_1 C_{ijkl}\varepsilon_{kl}+ \zeta_2{\color{black}\int_{\Omega}A(\rho)C_{ijkl}\varepsilon'_{kl}dv'}}}\]

Introducción

Métodos

Resultados

Parámetros del modelo no local

Factor no local

\[{\color{lightgray}\scriptsize{\sigma_{ij}= {\color{black}\zeta_1} C_{ijkl}\varepsilon_{kl}+ {\color{black}\zeta_2}\int_{\Omega}A(\rho)C_{ijkl}\varepsilon'_{kl}dv'}}\]

Representa que tanta no localidad se tiene en cuenta

\[\scriptsize{\zeta_1+\zeta_2=1}\]

$\zeta_1=1,\eta=1.78$

$\zeta_1=0.5,\eta=1.73$

$\zeta_1=0,\eta=0.28$

Notas presentación
- Factor no local z1
- Que tanta no localidad entra en juego
- Deben sumar 1
- Evita inestabilidades numéricas

Notas extendido
Modelo no local

Dichos aportes son ponderados usando los factores zeta (no se pronunciar zeta en griego, no hacer el ridículo.) Dar la tecla espacio
Estos factores representan un material compuesto de dos fases, por lo tanto, la suma de los dos factores debe ser 1. Dar espacio
Aquí deben salir los 3 modelos 3D. Mover uno de ellos con el mouse

En el modelo 1 se ve el primer modo de vibración de un cubo usando la teoría clásica (z1=1)
En el modelo 2 se ve el primer modo de vibración de un cubo usando la teoría no local (z1=0.5)
En el modelo 3 se ve el primer modo de vibración de un cubo usando (z1=0)

Frases obligatorias El zeta es muy relevante en la implementación computacional, ya que, de solo tener en cuenta la parte no local (z2=1) se llegan a irregularidades numéricas.

Introducción

Métodos

Resultados

Parámetros del modelo no local

Función de atenuación

\[{\color{lightgray}\scriptsize{\sigma_{ij}= \zeta_1 C_{ijkl}\varepsilon_{kl}+ \zeta_2\int_{\Omega}\color{black}A(\rho)\color{lightgray}C_{ijkl}\varepsilon'_{kl}dv'}}\]

Representa la relevancia de las fuerzas de cohesión de largo alcance. Depende de la distancia euclidiana ($|x-x'|$) y de la longitud interna ($l$)

\[\scriptsize{\rho=\frac{|x-x'|}{l}}\]

$A(\rho)=\lambda_0e^{-\rho}$

$A(\rho)=\lambda_0\left<1-\frac{\rho}{(1+\Omega_0)}\right>$

$A(\rho)=\lambda_0\left<1-\frac{\rho^2}{(1+\Omega_0)^2}\right>$

Notas presentación
- La parte no local depende de una función de atenuación
- Pondera las interacciones de largo alcance
- Depende de las distancias entre dos puntos del material
- Normalizada con la longitud interna
- Hay varios tipos
- A(0)=1
- A(oo)=0
- Función de probabilidad

Notas extendido
Modelo no local

El siguiente parámetro importante del modelo no local es la función de atenuación. Dar tecla espacio
Dicho parámetro pondera la relevancia de los efectos con respecto a la distancia. La función toma como parámetro la distancia euclidiana entre dos puntos (local y no local) normalizada por la longitud interna del material (parámetro no local del material). Dar tecla espacio
Las funciones de atenuación toman valores bajos a medidas que el parámetro de distancia aumenta. La idea es que modelen la atenuación de las interacciones entre puntos material a largas distancias.

Introducción

Métodos

Resultados

Parámetros del modelo no local

Función de atenuación

\[A(x,x',l)=\lambda_0e^{-\frac{|x-x'|}{l}}\]

El factor $\lambda_0$ es usado para garantizar las propiedades de la función. Este proceso es distinto para dominios 2D y 3D.

\[\scriptsize{\lambda_0\int_{\Omega_{\infty}}e^{\frac{-|x-x'|}{l}}d\Omega'=1}\]

2D

\[\small\lambda_0\int_{\Omega_{\infty}}e^{\frac{-|x-x'|}{l}}d\Omega'=t\lambda_0\int_{0}^{\infty}\int_{0}^{2\pi}re^{\frac{-r}{l}}{d\theta}{dr}\]

\[\small\lambda_0\int_{\Omega_{\infty}}e^{\frac{-|x-x'|}{l}}d\Omega'=\lambda_02\pi l^2t\]

\[\small\lambda_0=\frac{1}{2\pi l^2t}\]

3D

\[...=\lambda_0\int_{0}^{\infty}\int_{0}^{2\pi}\int_{0}^{\pi}r^2\sin(\phi)e^{\frac{-r}{l}}{d\phi}{d\theta}{dr}\]

\[...=\lambda_0 8\pi l^3\]

\[\lambda_0=\frac{1}{8\pi l^3}\]

Notas presentación
- Parámetros finales
- Función debe cumplir condición de la integral energía
- Distinto en 2D y 3D
- 2D: Polares y 3D: Esféricas

Notas extendido
Modelo no local

En resumen, la función de atenuación solamente depende de un punto local, un punto no local y la longitud interna del material. Presionar tecla espacio
Las funciones de atenuación tienen que cumplir con la condición de que la integral bajo un dominio infinito sea 1. Esto garantiza la conservación de la energía del método.
Dado que esta condición no se cumple con la función bi exponencial, es necesario aplicar un factor de corrección lambda0.
El procedimiento de encontrar dicho factor depende de la dimensión del modelo. Para este caso se muestra el proceso del caso bidimensional y tridimensional. Dar tecla espacio hasta terminar diapositiva

Frases obligatorias

La integral es impropia por el dominio infinito y converge por la exponencial

Introducción

Métodos

Resultados

Modelo de elementos finitos

FEM general

Para implementar elementos finitos es necesario seguir una serie de pasos

Enmallado (pre proceso)
Formulación variacional/Forma débil
Matrices y vectores de elementos
Ensamblaje de sistema de ecuaciones
Condiciones de borde
Solución del sistema de ecuaciones
Gráficas y productos (post proceso)

Introducción

Métodos

Resultados

Modelo de elementos finitos

FEM no local

Para implementar elementos finitos es necesario seguir una serie de pasos

Enmallado (pre proceso)
Detección elementos no locales
Formulación variacional/Forma débil
Matrices y vectores de elementos
Ensamblaje de sistema de ecuaciones
Condiciones de borde
Solución del sistema de ecuaciones
Gráficas y productos (post proceso)

Introducción

Métodos

Resultados

Formulación variacional/Forma débil

Se parte del modelo integral de dos fases y la ecuación de movimiento: $$\small\sigma_{ij}=\zeta_1 C_{ijkl}\varepsilon_{kl} + \zeta_2\int_{\Omega}A(\rho)C_{ijkl}\varepsilon'_{kl}dv'\\ \sigma_{ij,j}+f_i=0$$

Sustituyendo el modelo constitutivo en la ecuación de movimiento e integrando sobre el volumen ponderadamente (FEM) se obtiene: $$\small\int_{v}w\left(\frac{\partial}{\partial x_j}\left(\zeta_1 C_{ijkl}\varepsilon_{kl} + \zeta_2\int_{\Omega}A(\rho)C_{ijkl}\varepsilon'_{kl}dv'\right)+f_i\right)dv=0$$

Integrando por partes se puede llegar a expresiones para la matriz de rigidez de un elemento: $$\small K^e=\zeta_1\int_v B^T(x) C B(x)dv+\zeta_2\int_v\int_{v'} A(\rho) B^T(x) C B(x')dv'dv$$ En esta expresión la matriz $B$ hace referencia a las derivadas de las funciones de forma y la matriz $C$ al tensor de elasticidad del material.
Los efectos no locales afectan la rigidez pero no afectan la masa del sistema

Notas presentación
- Modelo constitutivo y ecuaciones de movimiento en su forma de esfuerzos
- Integral ponderada para elementos finitos. Integral de volumen
- Integrando por partes, gradiente
- Ecuaciones para la matriz de rigidez del elemento
- 2 partes, local y no local con z1
- No local es doble integral sobre el dominio
- No local tiene función de atenuación
- Masa no cambia

Notas extendido
FEM no local

Para encontrar las ecuaciones a nivel de elemento para implementar elementos finitos partimos de la ecuación constitutiva y de la ecuación de movimiento. Remplazando estas ecuaciones con las expresiones de deformaciones unitarias se obtiene un set de ecuaciones diferenciales acopladas. Estas ecuaciones acopladas se integran en el dominio, se multiplican por una función de ponderación y se igualan a cero para obtener la formulación integral ponderada que es necesaria para hacer elementos finitos. Posteriormente se integra por partes y se aplica el teorema del gradiente para obtener expresiones para la matriz de rigidez y el vector de fuerzas de elemento. Debido a que la ecuación constitutiva tiene una integral en el dominio, la expresión para matriz de elemento tendrá dos integrales. Esto obliga a realizar una doble integral sobre el dominio.

Introducción

Métodos

Resultados

Detección de elementos no locales

Función de atenuación biexponencial en 1D

Función de atenuación sobre elementos a una distancia Lr

Dado que $\rho$ se calcula como la distancia entre dos puntos, mientras mas lejos estén, menos importancia tienen

Elementos lejanos, tendrán $\rho\approx 0$, por lo tanto, solamente se necesitan tener en cuenta los elementos a una distancia < $Lr=6l$ (Polizzotto, 2001)

Introducción

Métodos

Resultados

Ensamblaje de sistema de ecuaciones

$$\small K^{nm}_{nl}=\begin{bmatrix} 300 & 125 & 425 & 28 \\ 125 & 250 & 542 & 425 \\ 425 & 542 & 250 & 125 \\ 28 & 425 & 125 & 300 \end{bmatrix} $$

$$\small K=\begin{bmatrix} {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} \\ {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{black}300} & {\color{black}125} & {\color{lightgray}x} & {\color{black}425} & {\color{black}28} & {\color{lightgray}x} \\ {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{black}125} & {\color{black}250} & {\color{lightgray}x} & {\color{black}542} & {\color{black}425} & {\color{lightgray}x} \\ {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} \\ {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{black}425} & {\color{black}542} & {\color{lightgray}x} & {\color{black}250} & {\color{black}125} & {\color{lightgray}x} \\ {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{black}28} & {\color{black}425} & {\color{lightgray}x} & {\color{black}125} & {\color{black}300} & {\color{lightgray}x} \\ {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} \\ {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} \\ {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} & {\color{lightgray}x} \end{bmatrix} $$

Notas presentación
- Para un elemento local existe varios elementos no locales
- Entre dos elementos (local y no local) existe un aporte
- El aporte no local de cada elemento al sistema es una matriz de multiples grados de libertad
- Se ensambla con los gdl de los dos elementos
- Aumenta el ancho de banda
- Disminuye la dispersion de la matriz (matriz se vuelve mas densa)
- Disminuye la dispersion de la matriz (matriz se vuelve mas densa)
- Mayor tiempo para solucionar

Notas extendido
FEM no local

En el caso no local, dado que las integrales se realizan cruzadas entre elementos, el ensamblaje de la matriz se realiza con los grados de libertad del elemento local y los grados de libertad del elemento no local. En este caso, los grados de libertad 2,3,5,6 y 4,5,7,8. Las matrices son simétricas, por lo que los datos que aparecen en la segunda matriz se repetirán en el sentido contrario.

Introducción

Métodos

Resultados

Proceso de elementos finitos completo

Diagrama de flujo del proceso de elementos finitos no local

Introducción

Métodos

Resultados

Validación de la implementación

La implementación del método se encuentra en un repositorio de GitHub: https://github.com/ZibraMax/FEM

Modelo objetivo. Adaptado de Pisano et al. (2009)

Comparación de $\varepsilon_x$ para $y=2.519$

Comparación de $\varepsilon_x$ para $x=0.019$

Introducción

Métodos

Resultados

Elementos no locales de un dominio de 5 elementos por lado

Elementos no locales de un dominio de 15 elementos por lado

Elementos no locales de un dominio de 25 elementos por lado

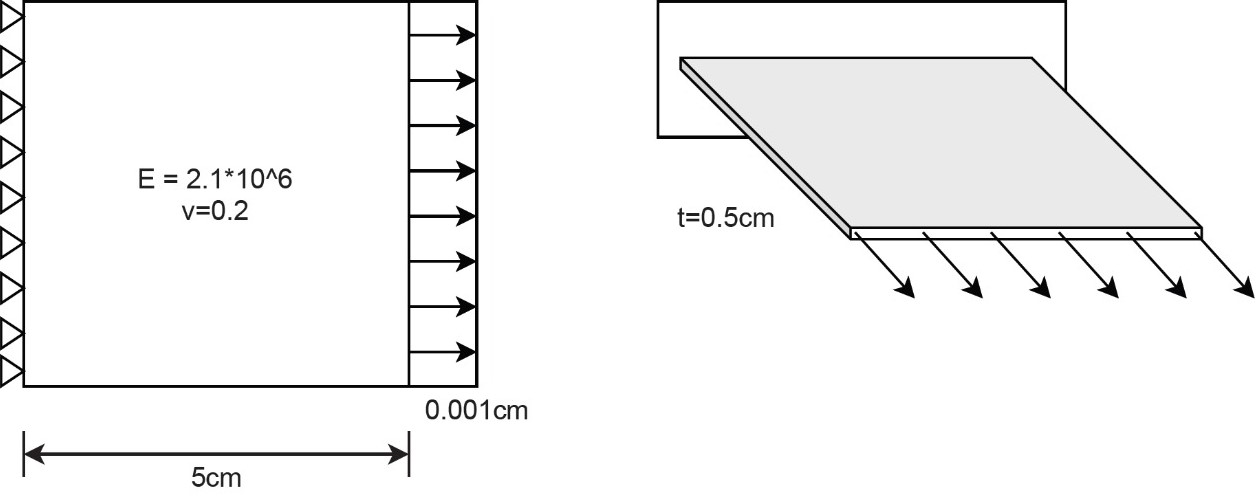
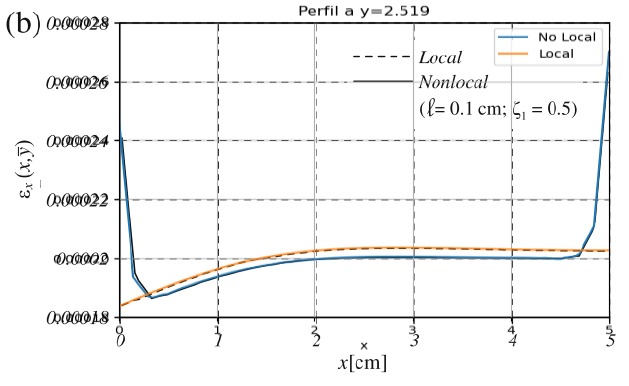
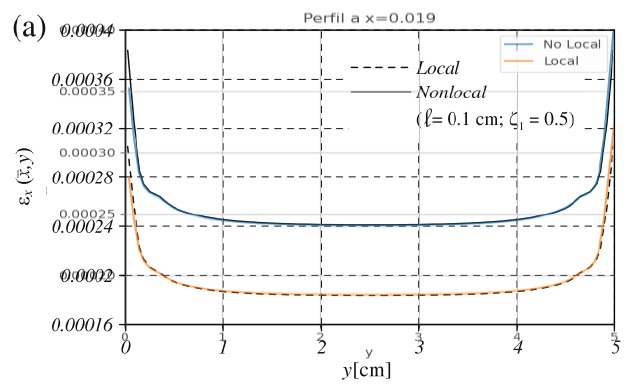
¿Qué tamaño hace que los efectos no locales sean despreciables?

Introducción

Métodos

Resultados

Simulaciones propuestas

Cubo de lado $R$

Placa cuadrada de lado $R$

Viga de longitud $R$

Con cada geometría:

Se varían los parámetros no locales $l$ y $\zeta_1$
Se cambia la distancia $R$
Se prueba con distintos materiales

Para cada caso se calcula la primera frecuencia natural $\omega$ usando teoría no local y la teoría no local

Introducción

Métodos

Resultados

Análisis de frecuencias normalizadas

Para comparar entre resultados se usa la frecuencia normalizada ($\eta $ ) $$\eta=\frac{\omega R}{C_t}$$

Donde $C_t$ es la velocidad de la onda de corte

Para cada simulación se realizan los siguientes pasos

Se calcula la frecuencia normalizada con la teoría no local $\eta_{nl}$
Se calcula la frecuencia normalizada con la teoría local $\eta_{l}$
Se calcula la diferencia relativa entre las frecuencias

$$\Delta=\left|\frac{\eta_{nl}-\eta_{l}}{\eta_{l}}\right|$$

Si $\Delta>5\%$ aumentar el tamaño $R$

Introducción

Métodos

Resultados

Materiales

Carbono

$\rho=3.515\ g/cm^3$

$$\scriptsize C=\begin{bmatrix} 1280.0 & 124.0 & 124.0 & 0 & 0 & 0 \\ 124.0 & 1280.0 & 124.0 & 0 & 0 & 0 \\ 124.0 & 124.0 & 1280.0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 578.0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 578.0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 578.0 \end{bmatrix}\ MPa$$

Silicio

$\rho=2.329\ g/cm^3$

$$\scriptsize C=\begin{bmatrix} 223.1 & 63.9 & 63.9 & 0 & 0 & 0 \\ 63.9 & 223.1 & 63.9 & 0 & 0 & 0 \\ 63.9 & 63.9 & 223.1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 79.6 & 0 & 0 \\ 0 & 0 & 0 & 0 & 79.6 & 0 \\ 0 & 0 & 0 & 0 & 0 & 79.6 \end{bmatrix}\ MPa$$

Germanio

$\rho=5.323\ g/cm^3$

$$\scriptsize C=\begin{bmatrix} 182.5 & 48.3 & 48.3 & 0 & 0 & 0 \\ 48.3 & 182.5 & 48.3 & 0 & 0 & 0 \\ 48.3 & 48.3 & 182.5 & 0 & 0 & 0 \\ 0 & 0 & 0 & 67.1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 67.1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 67.1 \end{bmatrix}\ MPa$$

Introducción

Métodos

Resultados

Procedimiento

Introducción

Métodos

Resultados

Resultados Preliminares

Introducción

Métodos

Resultados

Frecuencias normalizadas para cubos

Frecuencias para cubos usando teoría no local con $l=2,\zeta_1=0.5$

Introducción

Métodos

Resultados

Parámetros que se usarán en simulaciones de cubos

Longitud interna $l$

Se usan valores de $l = 0.1,0.5,1,2,5$

Tamaño $R$

Se usan valores de $R = 10l,15l,20l,50l,100l$

Factor no local $\zeta_1$

Se usan valores de $\zeta_1 = 0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.9,1.0$

Material

Se puede usar cualquiera, en este caso, carbono.

Introducción

Métodos

Resultados

Diferencia relativa de frecuencias no locales

Resultados para frecuencias normalizadas de cubos ($l=2,\zeta_1=0.5$)

Ajuste lineal con los primeros 5 puntos $$\eta_{nl}(R)=1.73-2.84\frac{1}{R}$$ Con $\eta_{l}=1.78$ se tiene: $$\Delta=\left|\frac{\eta_{nl}(R)-\eta_{l}}{\eta_{l}}\right|\%$$ Para conseguir $\Delta=5\%$ es necesario: $$R=34l$$

Introducción

Métodos

Resultados

Avance

Programa✅
Validación✅
Simulaciones para frecuencias (1 mes)
- Cubos✅
- Tetraedros
- Esferas
- Placas
- Vigas
Documento (1 mes)

Introducción

Métodos

Resultados

Referencias

Eringen, A. C. (1972). Linear theory of nonlocal elasticity and dispersion of plane waves. International Journal of Engineering Science, 10(5), 425–435. https://doi.org/10.1016/0020-7225(72)90050-X

Eringen, A. C. (1983). On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54(9), 4703–4710. https://doi.org/10.1063/1.332803

Eringen, A. C., & Edelen, D. G. B. (1972). On nonlocal elasticity. International Journal of Engineering Science, 10(3), 233–248. https://doi.org/10.1016/0020-7225(72)90039-0

Fleck, N. A., Muller, G. M., Ashby, M. F., & Hutchinson, J. W. (1994). Strain gradient plasticity: Theory and experiment. Acta Metallurgica et Materialia, 42(2), 475–487. https://doi.org/10.1016/0956-7151(94)90502-9

Ghorbani, K., Rajabpour, A., & Ghadiri, M. (2021). Determination of carbon nanotubes size-dependent parameters: Molecular dynamics simulation and nonlocal strain gradient continuum shell model. Mechanics Based Design of Structures and Machines, 49(1), 103–120. https://doi.org/10.1080/15397734.2019.1671863

Lam, D. C. C., Yang, F., Chong, A. C. M., Wang, J., & Tong, P. (2003). Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids, 51(8), 1477–1508. https://doi.org/10.1016/S0022-5096(03)00053-X

Introducción

Métodos

Resultados

Referencias

Naghinejad, M., & Ovesy, H. R. (2018). Free vibration characteristics of nanoscaled beams based on nonlocal integral elasticity theory. Journal of Vibration and Control, 24(17), 3974–3988. https://doi.org/10.1177/1077546317717867

Nguyen, N.-T., Kim, N.-I., & Lee, J. (2015). Mixed finite element analysis of nonlocal Euler–Bernoulli nanobeams. Finite Elements in Analysis and Design, 106, 65–72. https://doi.org/10.1016/j.finel.2015.07.012

Polizzotto, C. (2001). Nonlocal elasticity and related variational principles. International Journal of Solids and Structures, 38(42–43), 7359–7380. https://doi.org/10.1016/S0020-7683(01)00039-7

Ramirez, F. (2006). VIBRATION OF NANOSTRUCTURES: FROM ATOMIC TO CONTINUUM SCALES.

Sahmani, S., & Fattahi, A. M. (2018). Development of efficient size-dependent plate models for axial buckling of single-layered graphene nanosheets using molecular dynamics simulation. Microsystem Technologies, 24(2), 1265–1277. https://doi.org/10.1007/s00542-017-3497-3

Shariati, M., Azizi, B., Hosseini, M., & Shishesaz, M. (2021). On the calibration of size parameters related to non-classical continuum theories using molecular dynamics simulations. International Journal of Engineering Science, 168, 103544. https://doi.org/10.1016/j.ijengsci.2021.103544

Introducción

Métodos

Resultados

Referencias

Stölken, J. S., & Evans, A. G. (1998). A microbend test method for measuring the plasticity length scale. Acta Materialia, 46(14), 5109–5115. https://doi.org/10.1016/S1359-6454(98)00153-0

Wang, Y. B., Zhu, X. W., & Dai, H. H. (2016). Exact solutions for the static bending of Euler-Bernoulli beams using Eringen’s two-phase local/nonlocal model. AIP Advances, 6(8). https://doi.org/10.1063/1.4961695