FEM.Elements.E3D package#
Collection of 3D Elements
Submodules#
FEM.Elements.E3D.Brick module#
BRICK ELEMENTS#
Defines the lagrangian first order and second order brick elements
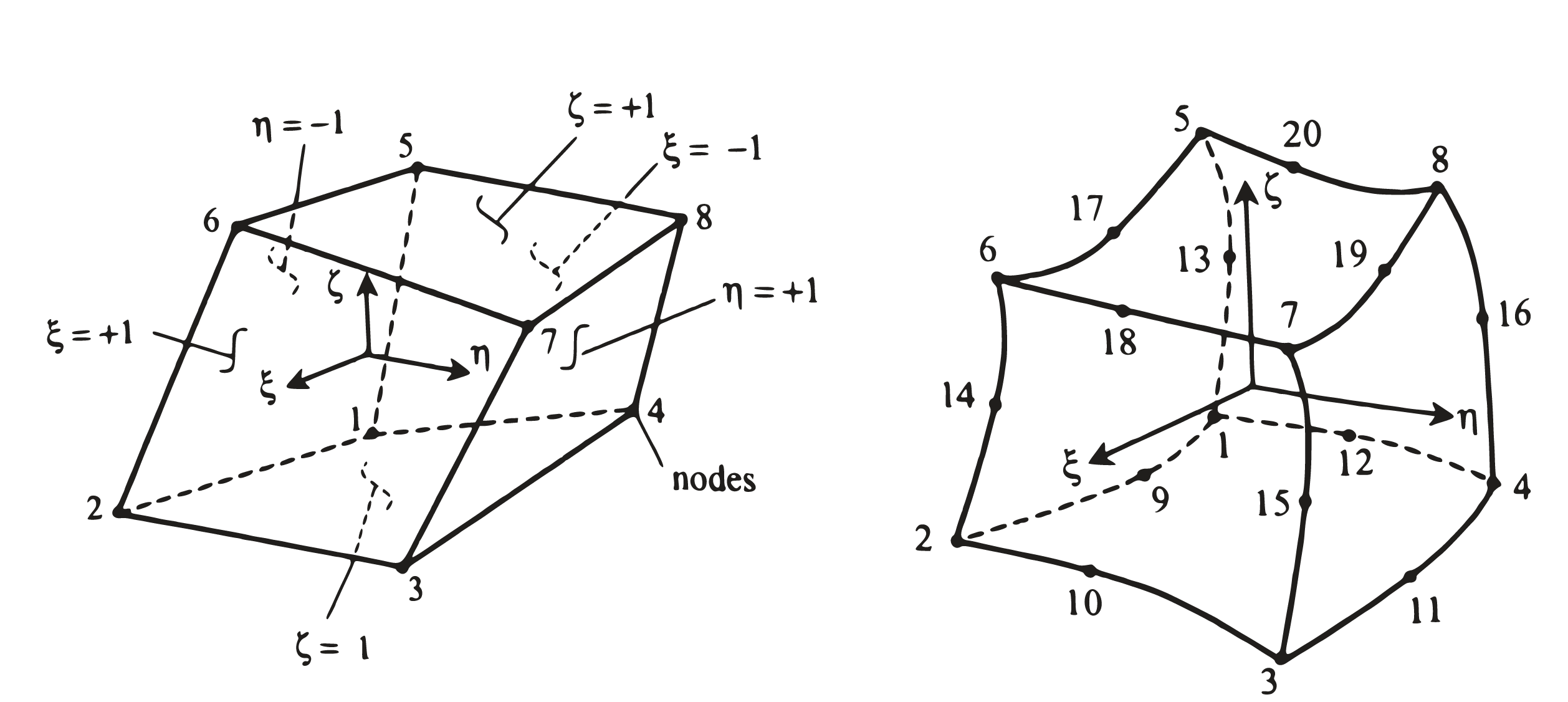
Brick (8 nodes) and BrickO2 (20 nodes). (Reddy, 2005)#
Brick#
First order 8 node brick element
Shape Functions#
Shape Functions Derivatives#
BrickO2#
Second order 20 node brick element
Shape Functions#
Shape Functions Derivatives#
- class FEM.Elements.E3D.Brick.Brick(coords: numpy.ndarray, gdl: numpy.ndarray, n: int = 3, **kargs)#
Bases:
FEM.Elements.E3D.Element3D.Element3D,FEM.Elements.E3D.BrickScheme.BrickSchemeCreates a 3D brick element
- Parameters
coords (np.ndarray) – Node coordinates matrix
gdl (np.ndarray) – Degrees of freedom matrix
n (int, optional) – Number of gauss points used for integration. Defaults to 3.
- dpsis(_z: numpy.ndarray) numpy.ndarray#
Calculates the shape functions derivatives of a given natural coordinates
- Parameters
z (np.ndarray) – Natural coordinates matrix
- Returns
Shape function derivatives evaluated in Z points
- Return type
np.ndarray
- psis(_z: numpy.ndarray) numpy.ndarray#
Calculates the shape functions of a given natural coordinates
- Parameters
z (np.ndarray) – Natural coordinates matrix
- Returns
Shape function evaluated in Z points
- Return type
np.ndarray
- class FEM.Elements.E3D.Brick.BrickO2(coords: numpy.ndarray, gdl: numpy.ndarray, n: int = 3, **kargs)#
Bases:
FEM.Elements.E3D.Element3D.Element3D,FEM.Elements.E3D.BrickScheme.BrickSchemeCreates a 3D second order brick element.
- Parameters
coords (np.ndarray) – Node coordinates matrix
gdl (np.ndarray) – Degrees of freedom matrix
n (int, optional) – Number of gauss points used for integration. Defaults to 3.
- dpsis(_z: numpy.ndarray) numpy.ndarray#
Calculates the shape functions derivatives of a given natural coordinates
- Parameters
z (np.ndarray) – Natural coordinates matrix
- Returns
Shape function derivatives evaluated in Z points
- Return type
np.ndarray
- psis(_z: numpy.ndarray) numpy.ndarray#
Calculates the shape functions of a given natural coordinates
- Parameters
z (np.ndarray) – Natural coordinates matrix
- Returns
Shape function evaluated in Z points
- Return type
np.ndarray
FEM.Elements.E3D.BrickScheme module#
Define the brick scheme used by brick elements
- class FEM.Elements.E3D.BrickScheme.BrickScheme(n: int, **kargs)#
Bases:
objectGenerate a brick integration scheme
- Parameters
n (int) – Number of gauss points
FEM.Elements.E3D.Element3D module#
Defines a general 2D element
- class FEM.Elements.E3D.Element3D.Element3D(coords: numpy.ndarray, _coords: numpy.ndarray, gdl: numpy.ndarray, **kargs)#
Bases:
FEM.Elements.Element.ElementCreate a 3D element
- Parameters
coords (np.ndarray) – Element coordinate matrix
_coords (np.ndarray) – Element coordinate matrix for graphical interface purposes
gdl (np.ndarray) – Degree of freedom matrix
- draw() None#
Create a graph of element
- isInside(x: numpy.ndarray) numpy.ndarray#
Test if a given points is inside element domain
- Parameters
x (np.ndarray) – Point to be tested
- Returns
Boolean array of test result
- Return type
np.ndarray
- jacobianGraph() None#
Create the determinant jacobian graph
FEM.Elements.E3D.Tetrahedral module#
TETRAHEDRAL ELEMENTS#
Defines the lagrangian first order and second order tetrahedral elements
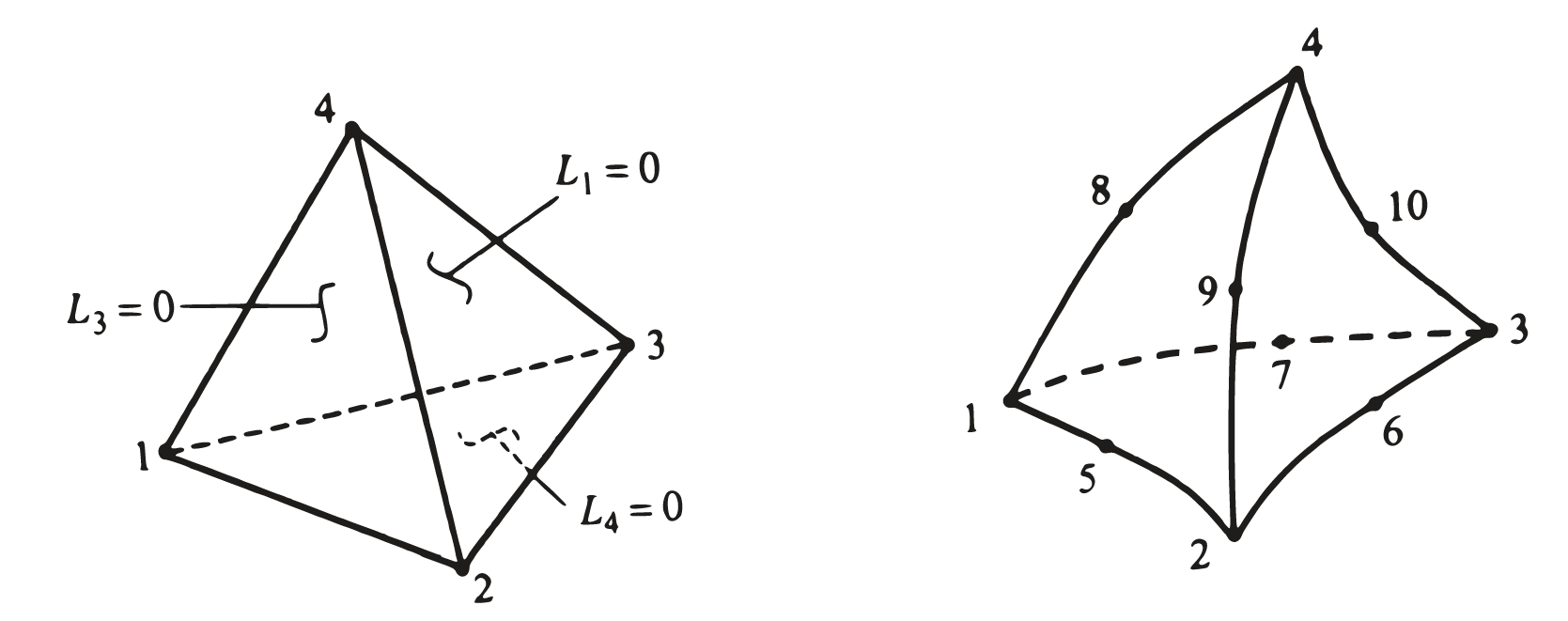
Tetrahedral (4 nodes) and TetrahedralO2 (10 nodes). (Reddy, 2005)#
Tetrahedral#
First order 4 node tetrahedral element
Shape Functions#
Shape Functions Derivatives#
TetrahedralO2#
Second order 10 node tetrahedral element
Shape Functions#
Shape Functions Derivatives#
- class FEM.Elements.E3D.Tetrahedral.Tetrahedral(coords: numpy.ndarray, gdl: numpy.ndarray, n: int = 3, **kargs)#
Bases:
FEM.Elements.E3D.Element3D.Element3D,FEM.Elements.E3D.TetrahedralScheme.TetrahedralSchemeCreates a 3D tetrahedral element
- Parameters
coords (np.ndarray) – Node coordinates matrix
gdl (np.ndarray) – Degrees of freedom matrix
n (int, optional) – Number of gauss points used for integration. Defaults to 3.
- dpsis(_z: numpy.ndarray) numpy.ndarray#
Calculates the shape functions derivatives of a given natural coordinates
- Parameters
z (np.ndarray) – Natural coordinates matrix
- Returns
Shape function derivatives evaluated in Z points
- Return type
np.ndarray
- psis(_z: numpy.ndarray) numpy.ndarray#
Calculates the shape functions of a given natural coordinates
- Parameters
z (np.ndarray) – Natural coordinates matrix
- Returns
Shape function evaluated in Z points
- Return type
np.ndarray
- class FEM.Elements.E3D.Tetrahedral.TetrahedralO2(coords: numpy.ndarray, gdl: numpy.ndarray, n: int = 3, **kargs)#
Bases:
FEM.Elements.E3D.Element3D.Element3D,FEM.Elements.E3D.TetrahedralScheme.TetrahedralSchemeCreates a 3D second order tetrahedral element
- Parameters
coords (np.ndarray) – Node coordinates matrix
gdl (np.ndarray) – Degrees of freedom matrix
n (int, optional) – Number of gauss points used for integration. Defaults to 3.
- dpsis(_z: numpy.ndarray) numpy.ndarray#
Calculates the shape functions derivatives of a given natural coordinates
- Parameters
z (np.ndarray) – Natural coordinates matrix
- Returns
Shape function derivatives evaluated in Z points
- Return type
np.ndarray
- psis(_z: numpy.ndarray) numpy.ndarray#
Calculates the shape functions of a given natural coordinates
- Parameters
z (np.ndarray) – Natural coordinates matrix
- Returns
Shape function evaluated in Z points
- Return type
np.ndarray
FEM.Elements.E3D.TetrahedralScheme module#
Define the tetrahedral scheme used by tetrahedral elements
- class FEM.Elements.E3D.TetrahedralScheme.TetrahedralScheme(n: int, **kargs)#
Bases:
objectGenerate a tetrahedral integration scheme
- Parameters
n (int) – Number of gauss points